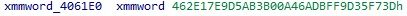WACON 2022 randomware 풀이
작년에 블로그가 없을 때 이 풀이를 쓰고 Github Gist 에 올려놨었는데, 이제 굳이 Gist 에 올릴 필요 없이 블로그에 올리면 되니 이 풀이도 블로그에 그대로 옮겨둔다.
Description
암호화된 파일들과 랜섬웨어류의 바이너리 하나가 주어진다.
암호화된 파일 리스트는 아래와 같다.
victim/ohhhhhhhhh.gif.xxx
victim/python_meme.png.xxx
victim/secret/THIS_IS_NOT_A_SECRET.txt.xxx
victim/secret/TOP_SECRET.pdf.xxx
Analysis
주어진 바이너리는 단순히 특정 디렉토리 내의 파일들을 모두 암호화하는 역할을 한다.
이 문제의 핵심은, 랜덤 값을 기반으로 암호화를 진행하는데 이 랜덤 값 생성 함수가 바이너리 내에 구현되어 있다. 따라서 복호화를 위해서는 우선 이 랜덤 함수를 분석하여 크랙해야 한다.
1. Cracking Random Function
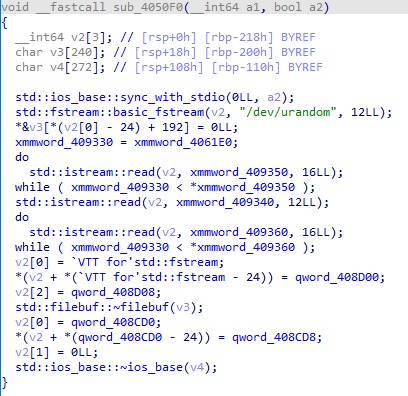
랜덤 함수는 sub_404FE0 으로, 코드는 아래와 같다.
먼저 이 코드의 동작을 분석해서 좀 더 보기 쉽게 코드를 재작성해보면 대략 아래와 같이 만들 수 있다.
def random():
global p, rnd1, rnd2, rnd3
result = 0
t1 = rnd3
t2 = rnd2
while True:
if (t2 & 1) == 1:
result = (result + t1) % p
t1 = (t1 * 2) % p
t2 >>= 1
if t2 == 0: break
rnd3 = (rnd1 + result) % p
return rnd3
위의 루프는 예전에 다른 CTF 들에서도 여러 번 봤던 형태로, 그냥 두 정수의 곱셈 연산이다. 따라서 더 깔끔하게 작성하면 아래와 같다.
def random():
global p, rnd1, rnd2, rnd3
rnd3 = rnd1 + ((rnd2 * rnd3) % p)
return rnd3
이렇게 보면 이 랜덤 함수가 LCG 라는 것을 명확하게 알 수 있다. 즉 문제를 풀기 위해서는 우선 LCG 를 크랙해야 한다. LCG 크랙은 해본 적이 없었기 때문에 검색을 해본 결과 이 사이트를 찾을 수 있었다. 해당 사이트에서는 LCG 크랙에 대해 완벽하게 설명하고 있다. 실제로 샘플 데이터를 만들어서 테스트를 해보면 크랙이 되는 것을 볼 수 있다.
그러나 위 사이트의 내용대로 바로 크랙을 할 수는 없는데, 한 가지 문제가 있다. 우선 위 함수에서 쓰이는, LCG 에 필요한 변수들의 초기값을 설정하는 루틴을 보면 아래와 같다.
이 함수는 프로그램이 시작하면서 호출되는데, 16bytes 값 2개와 12bytes 값 1개를 /dev/urandom 을 통해 설정한다. LCG 는 총 3가지 변수가 필요한데, 위의 16bytes 값 중 하나는 seed 이므로 제외하면 변수 하나가 남는데, 이 하나는 0x4061E0 주소에서 가져오고 그 값은 아래와 같다.
이 값은 고정되어 있는데, 이 변수가 쓰이는 곳을 보면 LCG 에서 modulus(위의 Python 코드에서 p) 변수라는 것을 알 수 있다. 즉 modulus 는 이미 알고 있는 상태이고 크랙해야 하는 것은 multiplier 와 increment 두 변수이다. 이 경우 위 사이트의 Challenge 2: unknown increment and multiplier 에 나와있는 대로 크랙을 해야 한다.
그러나 위 사이트의 내용을 보면 이 경우의 크랙을 위해서는 연속된 3개의 랜덤 결과값을 요구하며, 제시된 수식과 코드도 그 경우에 맞춰서 작성되어 있다. 이 바이너리에서 파일 하나를 암호화하는 데에 LCG 를 몇 번 호출하는지 보면 아래와 같다.
총 4번 호출하는데, 그 중 가장 먼저 호출해서 얻는 랜덤 값(16bytes)은 암호화된 파일의 시작 부분에 쓰여진다. 그 외의 나머지 3개 값은 파일에 쓰여지지 않기 때문에 알 수 없다. 이 문제는 암호화된 파일이 총 4개가 주어진다. 이를 바탕으로 LCG 함수가 호출되는 순서와 알 수 있는 값을 정리하면 아래와 같다.
lcg() - 1번째 파일
lcg() - ?
lcg() - ?
lcg() - ?
lcg() - 2번째 파일
lcg() - ?
lcg() - ?
lcg() - ?
lcg() - 3번째 파일
lcg() - ?
lcg() - ?
lcg() - ?
lcg() - 4번째 파일
lcg() - ?
lcg() - ?
lcg() - ?
보다시피 연속된 랜덤 값을 알 수는 없고 위처럼 불연속적인 값만 알 수 있다. 다행히 위 사이트에서는 어떻게 크랙을 하는지 수식을 구체적으로 적어놓았기 때문에 이를 바탕으로 불연속적인 값으로도 크랙이 가능할지 생각을 해볼 수 있다. 위 사이트에 나와있는 수식은 아래와 같다.
\[\begin{align} s_1&=s_0m+c&\pmod{n} \\ s_2&=s_1m+c&\pmod{n} \\\\ s_2-s_1&=s_1m-s_0m&\pmod{n} \\ &=m(s_1-s_0)&\pmod{n} \\\\ m&=\frac{s_2-s_1}{s_1-s_0}&\pmod{n} \end{align}\]이 수식을 바탕으로 해야 하는 것은, $m$ 을 표현하는 최종 식에 $s_0$, $s_4$, $s_8$ 등 이미 값을 알고 있는 변수만으로 이루어지는 수식이 되도록 치환하는 것이다. 사실 이것은 매우 단순한데, 식의 개수를 늘리고 비슷한 흐름으로 식을 만들어보면 아래와 같다.
\[\begin{align} s_1&=s_0m+c&\pmod{n} \\ &... \\ s_8&=s_7m+c&\pmod{n} \\\\ s_4&=(((s_0m+c)m+c)m+c)m + c&\pmod{n} \\ &=s_0m^4+cm^3+cm^2+cm+c&\pmod{n} \\ s_8&=(((s_4m+c)m+c)m+c)m + c&\pmod{n} \\ &=s_4m^4+cm^3+cm^2+cm+c&\pmod{n} \\\\ s_8-s_4&=s_4m^4-s_0m^4&\pmod{n} \\ &=m^4(s_4-s_0)&\pmod{n} \\\\ m^4&=\frac{s_8-s_4}{s_4-s_0}=(s_8-s_4)*modinv(s_4-s_0)&\pmod{n} \end{align}\]이렇게 하면 결과적으로 우변의 값은 모두 이미 알고 있는 값들로만 이루어지므로 계산이 가능하게 되고, 하나의 상수(이하 $a$)가 된다. 보다시피 이는 결국 $m$ 이 $m^4$ 가 된 것을 제외하면 원래의 식과 다를 바 없는 동일한 식이다. 위 식을 다시 쓰면 아래와 같다. (바이너리에 고정되어 있던 modulus 값은 소수이므로 p 로 표기)
\[x^4=a\pmod{p}\]결국 이 식에서 $x$ 를 구하라는 것과 같다. 이는 고민할 필요 없이 Wolframalpha 에게 맡기도록 한다. 결과적으로 이 계산식은 위에 언급했듯이 $m$ 이 $m^4$ 로 바뀐 것을 제외하면 원래의 식과 동일하기 때문에, $a$ 를 구하는 것은 위 사이트의 코드를 그대로 쓸 수 있다.
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
def modinv(b, n):
g, x, _ = egcd(b, n)
if g == 1:
return x % n
def get_a(states, modulus):
a = (states[2] - states[1]) * modinv(states[1] - states[0], modulus) % modulus
return a
암호화된 파일 순서는 파일명 순으로 가정해서 $s_0$, $s_4$, $s_8$ 를 뽑았다. 그러면 아래와 같이 호출하면 $a$ 를 얻을 수 있다.
p = 0x462e17e9d5ab3b00a46adbff9d35f73d
s0 = 0x3a82ca5851a6dd7b3eee35341dd57b88
s4 = 0x3ed6df7991dbe7886265daf32a27dc6c
s8 = 0x43c60e89bd061454e47b8d70b61f6d02
print(get_a([s0, s4, s8], p))
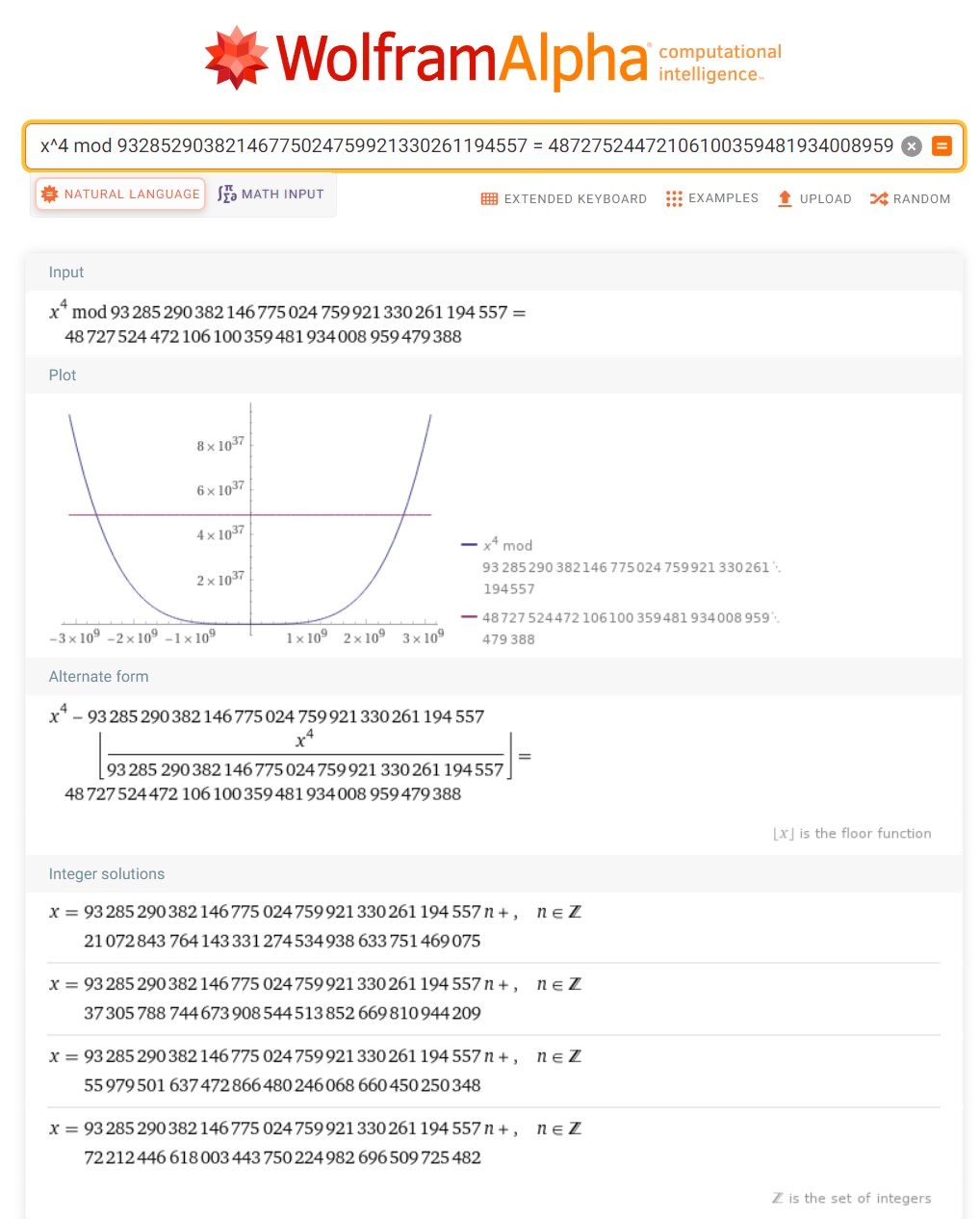
얻은 $a$ 값으로 Wolframalpha 에 그대로 식을 넣어보면 아래와 같은 결과를 얻을 수 있다.
4개의 근을 얻을 수 있는데, 이 중 뭐가 맞는지는 알 수 없으니 그냥 4개 다 각각 사용해서 LCG 를 돌려보고 올바른 랜덤 값이 나오면 그 근이 맞는 것이니 그걸 사용하면 된다.
이제 multiplier 를 구했으니 남은 건 increment 를 구하면 된다. 방식은 위와 동일하게 수식에서 아는 값만 남도록 적절히 치환하면 된다.
\[\begin{align} s_4&=(((s_0m+c)m+c)m+c)m+c&\pmod{n} \\ &=s_0m^4+cm^3+cm^2+cm+c&\pmod{n} \\ &=s_0m^4+c(m^3+m^2+m+1)&\pmod{n} \\\\ s_4-s_0m^4&=c(m^3+m^2+m+1)&\pmod{n} \\\\ c&=\frac{s_4-s_0m^4}{m^3+m^2+m+1}=(s_4-s_0m^4)*modinv(m^3+m^2+m+1)&\pmod{n} \end{align}\]$m$ 을 구했기 때문에 $c$ 도 간단하게 구할 수 있다. Python 으로 쓰면 아래와 같다.
p = 0x462e17e9d5ab3b00a46adbff9d35f73d
m = 0x1c10d5647739358244cf60daaff7a8d1
s0 = 0x3a82ca5851a6dd7b3eee35341dd57b88
s4 = 0x3ed6df7991dbe7886265daf32a27dc6c
s8 = 0x43c60e89bd061454e47b8d70b61f6d02
print((s4 - (s0 * (m ** 4))) * modinv(m ** 3 + m ** 2 + m + 1, p) % p)
실행하면 increment 값을 얻을 수 있다. 사실 위의 4개의 근 중 어떤 $m$ 이 올바른 값인지 이 단계에서 바로 알 수 있는데, increment 는 12bytes 이므로 위의 올바른 $m$ 에서만 상당히 작은 수가 나오는 것을 볼 수 있다.
이렇게 LCG 에 필요한 모든 변수는 다 준비되었다.
p = 0x462e17e9d5ab3b00a46adbff9d35f73d
m = 0x1c10d5647739358244cf60daaff7a8d1
a = 0xa32ed02038c95b44a1a0009b
s0 = 0x3a82ca5851a6dd7b3eee35341dd57b88
물론 실제 초기 seed 값은 알 수 없으나, 당연히 처음 랜덤 값인 s0 만 있어도 충분하다.
2. Decrypt
이제 랜덤 함수를 크랙했으니 남은 것은 암호화 루틴을 분석해서 복호화를 하는 것이다. 위에도 첨부한 이미지를 다시 보면 아래와 같다.
여기서 암호화에 관련된 함수는 sub_404BD0 과 sub_404CC0 이다. 먼저 sub_404BD0 함수를 보자.
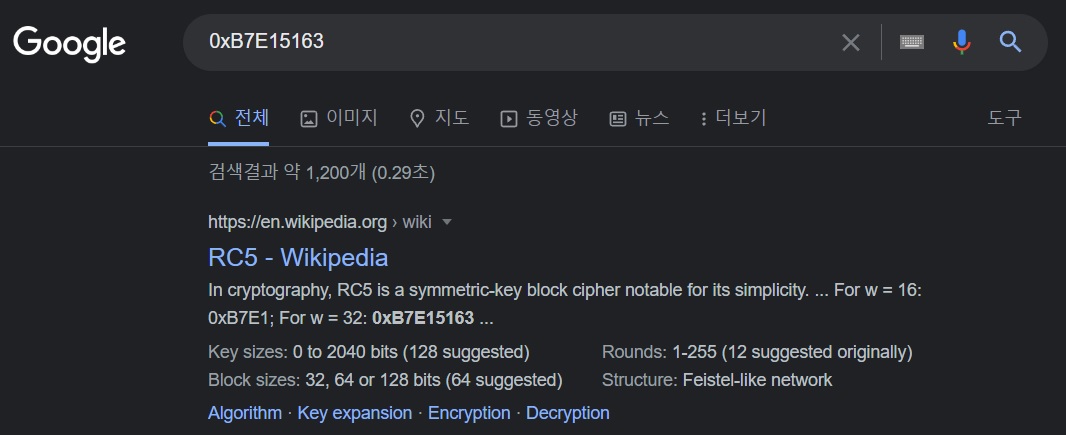
위를 보면 시그니처 값으로 보이는 0xB7E15163 과 0x61C88647 등의 값들이 있다. 이 값을 구글링해보면 아래와 같은 결과를 볼 수 있다.
물론 검색할때마다 순서는 매번 다르겠지만, CTF 당시에 검색했을 때는 위와 같이 제일 위에 RC5 가 나왔었다. 그리고 실제로 이 값은 RC5 암호화의 키 생성에서 쓰인다. 그래서 여기서 쓰이는 암호화가 RC5 라고 추측을 할 수 있다. 후술하겠지만 이는 치명적인 오판이었다.
암호화 종류를 파악했다고 생각했으므로 굳이 분석할 필요 없이 테스트를 해보기로 하고, libtomcrypt 라는 적절한 라이브러리를 찾아서 이를 이용해 아래와 같은 간단한 코드를 작성했다.
#include <tomcrypt.h>
int main()
{
unsigned char k[20] = { 0, };
unsigned char pt[20] = "aaaaaaaaaaaaaaaa";
symmetric_key skey;
rc5_setup(k, 16, 21, &skey);
for (int i = 0; i < 44; i++)
printf("0x%08X, ", skey.rc5.K[i]);
return 0;
}
위의 인자로 넘겨주는 16 과 21 은 각각 keysize 와 round 횟수이다. 사실 코드 분석을 해보면 실제로는 20 round 인데, 20 을 넘겨주니 실제 바이너리에서 돌렸을 때의 키 배열과 맞지 않아서 round 를 1 부터 쭉 돌려서 같은 키 배열이 나올 때까지 반복했더니 round 가 21 일 때 바이너리와 동일한 K 배열이 형성되어서 저렇게 설정한 것이다.
여기서 이미 무언가 이상하다는 것을 깨달아야 했으나, 하필 21 이라도 일단 같은 값이 나온다는 것에서 RC5 가 맞다는 확신을 가지게 되어 다른 생각을 하지 않았다. 그러나 이것을 바탕으로 실제로 RC5 암/복호화 테스트를 해보면 아무리 해도 같은 결과 값이 나오지 않았다. 이 단계에서 이제는 아예 이 암호화가 RC5 를 출제자가 약간 변형한 커스텀 암호화가 아닐까 하는 생각까지 가게 되었다.
그래서 암호화 함수(sub_404CC0)를 분석해서 Python 으로 간략하게 만들었다.
def ROL(data, shift, size=32):
shift %= size
remains = data >> (size - shift)
body = (data << shift) - (remains << size)
return (body + remains)
def ROR(data, shift, size=32):
shift %= size
body = data >> shift
remains = (data << (size - shift)) - (body << size)
return (body + remains)
def encrypt(m, key):
A = m[0]
B = m[2]
C = (m[1] + key[0]) % (2 ** 32)
D = (m[3] + key[1]) % (2 ** 32)
tD = B
for i in range(1, 21):
tC = C
B = tD
tD = D
t1 = (C * (2 * C + 1)) % (2 ** 32)
t2 = (D * (2 * D + 1)) % (2 ** 32)
C = (ROL(B ^ ROL(t2, 5), t1 >> 27) + key[i * 2 + 1]) % (2 ** 32)
D = (ROL(A ^ ROL(t1, 5), t2 >> 27) + key[i * 2]) % (2 ** 32)
A = tC
print(hex((key[42] + A) % (2 ** 32)))
print(hex(C))
print(hex((key[43] + tD) % (2 ** 32)))
print(hex(D))
k = [0x2A66311C, 0x9B17852D, 0x8108B207, 0x39D14185, 0x9C64DF5F, 0x4BED6BCD, 0xB1D88726, 0x4E6EE8C6, 0x66F7FA9C, 0x429C2724, 0xC955B6BF, 0x9306E49A, 0x75524DD9, 0x56F4DA3C, 0x5EC06B9B, 0xABBC779B, 0x15EE39A1, 0x66E7755F, 0x0025068D, 0x7CB6D760, 0xA6B4A4BE, 0x11B98FB8, 0x512B019F, 0x5A199FCE, 0xBD468F9E, 0x1DB66D3A, 0x61B5D390, 0x84BFED42, 0x8690AEE8, 0x774B9EE5, 0x9FD534B1, 0x848939E0, 0x62A03756, 0xFD977349, 0x59ABCDCA, 0xC8AF1E91, 0x8E6D2107, 0x359B2C7D, 0x63018004, 0xC7B27AE3, 0x55FCC1B3, 0xC5BD8DB7, 0x05B4016A, 0x4B38AC83]
p = [0x61616161, 0x61616161, 0x61616161, 0x61616161]
encrypt(p, k)
이렇게 해놓고 보면 암호화 루틴이 RC5 와 약간 비슷하지만 확실히 다르다. 이 암호화 함수의 형태를 보고 RC5 와 유사하게 적당히 대칭적인 형태로 복호화 함수를 추정해서 만들기 위해, 우선 방해가 되는 임시 변수들을 없애고 깔끔하게 만드는 데에 남은 시간을 다 들였으나 결국 CTF 가 끝날 때까지 완료하지 못하고 종료되었다.
이후 약 2주가 지나도록 풀이가 나오지 않아서 그냥 직접 풀기로 하고, 이 단계에서부터 다시 생각을 하였다. 그러다가 RC6 암호화 위키백과 페이지의 코드를 보게 되었다.
for i = 1 to r do
{
t = (B * (2B + 1)) <<< lg w
u = (D * (2D + 1)) <<< lg w
A = ((A ^ t) <<< u) + S[2i]
C = ((C ^ u) <<< t) + S[2i + 1]
(A, B, C, D) = (B, C, D, A)
}
저 (B * (2B + 1)) 부분을 보고, 이 문제의 암호화가 RC6 라는 것을 확신하게 되었다. 사실 RC6 도 물론 CTF 당시에 보기는 했으나, 그 때는 저렇게 Python 으로 코드를 정리하기 전이었기 때문에 위의 RC6 암호화 루틴의 형태만 보고 바로 확신하기는 어려웠던 것 같다.
어쨌든 그래서 이 암호화는 RC6 이고, 위에서 했던 암호화 키 생성 테스트는 사실 아래와 같이 해도 동일한 결과를 얻는다.
#include <tomcrypt.h>
int main()
{
unsigned char k[20] = { 0, };
unsigned char pt[20] = "aaaaaaaaaaaaaaaa";
symmetric_key skey;
rc6_setup(k, 16, 20, &skey);
for (int i = 0; i < 44; i++)
printf("0x%08X, ", skey.rc6.K[i]);
return 0;
}
이제 RC6 함수로 암/복호화 테스트를 해보면 정상적으로 문제 바이너리에서와 동일한 결과를 얻을 수 있다. 다시 암호화 루틴으로 돌아가보자.
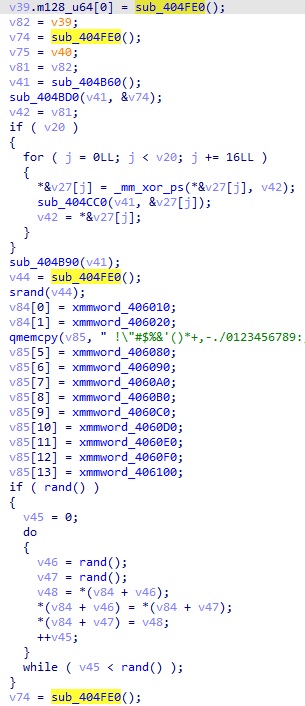
위 코드에서 알 수 있다시피 CBC 방식이고, IV 는 위에서 서술했지만 파일의 제일 앞에 쓰여지는 16bytes 의 랜덤 값이다. 그래서 이 부분은 아무 문제없이 쉽게 넘어갈 수 있다. 다음 루틴에서 srand 의 인자로 랜덤 값을 생성해서 넘겨주는 것을 볼 수 있는데, 물론 이미 LCG 를 크랙했으므로 이후 호출하는 rand 함수들에 대해서는 전부 동일한 값을 얻어낼 수 있다.
그리고 이제 다음을 보면 아래와 같은 복잡한 루틴이 있다.
위에서부터 2개의 루프는 사실 0 부터 256 까지 순서대로 채워진 256bytes 배열을 이리저리 조작하는 일종의 키 테이블 세팅에 불과한 부분이고, 마지막 루프에서 v27 은 앞에서 RC6 암호화를 하고 난 후의 암호화 데이터이다.
즉 복잡해보이지만 실제로는 결국 RC6 암호화 데이터를 정직하게 1바이트씩 특정한 값들로 xor 을 하는 것이다. 그리고 그 xor 하는 키 배열을 결정하는 것은 결국 rand 함수이다. 결국 저 루틴을 일일이 분석할 필요 없이 srand 인자만 동일하게 맞춰주고, 저 루틴을 통째로 복사해서 어떤 값으로 xor 을 하는지 미리 저장해놓기만 하면 쉽게 역연산을 할 수 있는 것이다.
3. Run
이를 바탕으로 최종 풀이 코드를 작성했다. bigint 연산을 위해 libgmp 를 사용했다.
#include <stdint.h>
#include <tomcrypt.h>
#include <gmp.h>
typedef unsigned char _BYTE;
mpz_t p, m, a, s;
void lcg(mpz_t r)
{
mpz_init(r);
if (!mpz_cmp_ui(s, 0)) {
mpz_init_set_str(s, "3a82ca5851a6dd7b3eee35341dd57b88", 16);
mpz_set(r, s);
}
else {
mpz_init(r);
mpz_mul(r, m, s);
mpz_mod(r, r, p);
mpz_add(r, r, a);
mpz_set(s, r);
}
}
void get_xorkey(_BYTE* key, __int128 r1, __int128 r2, int n)
{
srand(r1);
unsigned char v85[260];
for (int i = 0; i < 256; i++)
v85[i] = i;
_BYTE v46, v48, v52, v53, v54, v57 = 0, v58;
int v45 = 0, v47 = 0, idx = 0, v51 = 0;
if (rand())
{
do
{
v46 = (_BYTE)rand();
v47 = (_BYTE)rand();
v48 = *((_BYTE*)v85 + v46);
*((_BYTE*)v85 + v46) = *((_BYTE*)v85 + v47);
*((_BYTE*)v85 + v47) = v48;
++v45;
} while (v45 < (_BYTE)rand());
}
do
{
v52 = *((_BYTE*)v85 + idx);
v53 = v52 + v51 + *((_BYTE*)&r2 + (idx & 0xE));
*((_BYTE*)v85 + idx) = *((_BYTE*)v85 + v53);
*((_BYTE*)v85 + v53) = v52;
v54 = *((_BYTE*)v85 + idx + 1);
v51 = (_BYTE)(v53 + v54 + *((_BYTE*)&r2 + ((idx + 1) & 0xF)));
*((_BYTE*)v85 + idx + 1) = *((_BYTE*)v85 + v51);
*((_BYTE*)v85 + v51) = v54;
idx += 2;
} while (idx != 256);
for (long long v56 = 0; v56 < n; v56++) {
v58 = *((_BYTE*)v85 + (_BYTE)(v56 + 1));
v57 += v58;
*((_BYTE*)v85 + (_BYTE)(v56 + 1)) = *((_BYTE*)v85 + v57);
*((_BYTE*)v85 + v57) = v58;
key[v56] = *((_BYTE*)v85 + (_BYTE)(v57 + *((_BYTE*)v85 + (_BYTE)(v56 + 1))))
+ *((_BYTE*)v85 + (_BYTE)(*((_BYTE*)v85 + (_BYTE)(v56 + 1)) + v58))
+ *((_BYTE*)v85
+ ((_BYTE)(*((_BYTE*)v85
+ ((v57 >> 3) | (unsigned int)(_BYTE)(32 * (v56 + 1))))
+ *((_BYTE*)v85
+ (((_BYTE)(v56 + 1) >> 3) | (unsigned int)(_BYTE)(32 * v57)))) ^ 0xAALL));
}
}
int main()
{
_BYTE k[32], *pt, *ct, *key;
mpz_init(s);
mpz_init_set_str(a, "a32ed02038c95b44a1a0009b", 16);
mpz_init_set_str(m, "1c10d5647739358244cf60daaff7a8d1", 16);
mpz_init_set_str(p, "462e17e9d5ab3b00a46adbff9d35f73d", 16);
for (int i = 0; i < 3; i++) {
mpz_t temp;
lcg(temp);
lcg(temp);
lcg(temp);
lcg(temp);
}
FILE* fp = fopen("TOP_SECRET.pdf.xxx", "rb");
fseek(fp, 0, SEEK_END);
int n = ftell(fp) - 16;
pt = malloc(n + 16);
ct = malloc(n + 16);
key = malloc(n + 16);
fseek(fp, 0, SEEK_SET);
fread(ct, 1, 16, fp);
fread(ct, 1, n, fp);
fclose(fp);
mpz_t iv, iv2, ik;
lcg(iv);
lcg(ik);
mpz_export(k, NULL, -1, 1, 0, 0, ik);
symmetric_key skey;
rc6_setup(k, 16, 20, &skey);
_BYTE r1s[20] = { 0, }, r2s[20] = { 0, };
mpz_t r1, r2;
lcg(r1);
lcg(r2);
mpz_export(r1s, NULL, -1, 1, 0, 0, r1);
mpz_export(r2s, NULL, -1, 1, 0, 0, r2);
get_xorkey(key, *(__int128*)r1s, *(__int128*)r2s, n);
for (int i = 0; i < n; i++)
ct[i] ^= key[i];
rc6_setup(k, 16, 20, &skey);
for (int i = 0; i < n; i += 16) {
mpz_t t;
mpz_init(iv2);
mpz_import(iv2, 16, -1, 1, 0, 0, ct + i);
rc6_ecb_decrypt(ct + i, pt + i, &skey);
mpz_init(t);
mpz_import(t, 16, -1, 1, 0, 0, pt + i);
mpz_xor(t, t, iv);
mpz_set(iv, iv2);
mpz_export(pt + i, NULL, -1, 1, 0, 0, t);
}
fp = fopen("output", "wb");
fwrite(pt, 1, n, fp);
fclose(fp);
return 0;
}
위 코드는 TOP_SECRET.pdf.xxx 를 대상으로 하고 있는데, 이 파일은 파일명 순서상으로 가장 마지막에 암호화되었기 때문에 미리 앞에서 LCG 를 4 * 3 번 호출해주고 있다. 다른 파일을 복호화하려면 파일명 순서대로 LCG 를 4 * n 번씩 호출하면 된다.(n=0, 1, 2, 3)
이유는 모르겠으나, txt 파일을 제외한 다른 두 이미지 파일은 깨진 느낌으로 나오는데 원래 이런 것인지 무언가 잘못된 것인지는 모르겠다. txt 파일은 그냥 Lorem Ipsum 텍스트이다.
마지막인 TOP_SECRET.pdf.xxx 를 복호화해서 열어보면 아래와 같은 페이지를 볼 수 있다. 드래그해서 복사하면 정상적으로 플래그를 얻을 수 있다.